Basic Statistics
In statistics mean, median and mode are all measures of central tendency. These values help to interpret data. Each of these, mean, median and mode, provide more insight into the data. These are all measures of central tendency yet, there are differences in each one of these values.
What is the Mean, Median and Mode?
Let’s define these three terms.
• The mean is the arithmetic average of a set of given numbers. Therefore, the mean is often simply referred to as the ‘average’.
• The median is the middle score in a set of given numbers. As the median, half of the scores are above this number and half are below.
• The mode is the most frequently occurring score in a set of given numbers. Put in another way, it is the score that appears the greatest number of times.
Mean
In its simplest mathematical or statistical definition, the mean is referred to as the mathematical expectation of average. The equation for calculating the mean is the sum of all values in the data set, divided by the total number of values. This is one of the simplest definitions of the mean.
How to Find the Mean ?
The mean is found using by adding up all of the numbers and dividing by the total number of numbers in the data set.
1. Add up all data values to get the sum
2. Count the number of values in your data set
3. Divide the sum by the count
The mean is the same as the average value.
Ex. 1.
Calculate the mean from the following number set:
5, 11, 4, 6, 8, 9, 6.
To calculate the mean first add all the numbers together
(5 + 11 + 4 + 6 + 8 + 9 + 6 = 49).
Then divide the total sum by the number of scores
(49 / 7 = 7).
In this example, the mean or average of the number set is 7
Ex. 2.
Given the data set 10, 12, 38, 23, 38, 23, 24, applying the above steps yields:
10, 12, 38, 23, 38, 23, 24 = 168, 168 / 7 = 24
(Mean is calculated by adding all the scores together, then dividing by the number of scores.)
In this example, the mean or average of the number set is 24.
The mean is often denoted as x̄, pronounced ‘x bar’. It is calculated by the use of the
following formula:
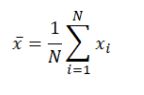
Median
The median is the central number of a data set. The statistical concept of the median is a value that divides a data sample or population distribution into two halves. Finding the median essentially involves finding the value in a data sample that has a physical location between the rest of the numbers. When calculating the median of a finite list of numbers, the order of the data samples is important. (Conventionally, the values are listed in ascending order.) In the case where the total number of values in a data sample is odd, the median is simply the number in the middle of the list of all values. When the data sample contains an even number of values, the median is the mean of the two middle values.
How to Find the Median ?
The median is the data value separating the upper half of a data set from the lower half.
1. Arrange data values from lowest to the highest value
2. The median is the data value in the middle of the set
3. If there are 2 data values in the middle the median is the mean of those 2 values.
Ex. 1.
Calculate the mean from the following number set:
The median for the data set 1, 1, 2, 5, 6, 6, and 9, the median is 5.
For the data set 1, 1, 2, 6, 6, 9 the median is 4.
(Take the mean of 2 and 6 or, (2+6) / 2 = 4.)
Ex. 2.
Given the same data set as before, the median would be acquired in the following manner:
2, 10, 23, 23, 24, 38, 38
After listing the data in ascending order, and determining that there are an odd number of values, it is clear that 23 is the median in this case. If there were another value added to the data set:
2,10, 23, 23, 24, 38, 38, 40
Since there are an even number of values, the median will be the average of the two middle numbers, in this case, 23 and 24, the mean of which is 23.5.
Mode
The mode is the number in a data set that occurs most frequently. In statistics, the mode is the value in a data set that has the highest number of recurrences. Of all the measures, finding the mode requires the least amount of mathematical calculation. Instead, since the mode is simply the most frequently occurring score in a distribution, it is just to look at all the scores and select the most common one.
How to Find the Mode ?
1. Look at all the data scores
2. Identify the data score that appears most often
Ex. 1.
consider the following number distribution:
2, 3, 6, 3, 7, 5, 1, 2, 3, 9.
The mode of these numbers would be 3 since this is the most frequently occurring number
(2,3, 6, 3, 7, 5, 1, 2, 3, 9).
(Mode is the value or values in the data set that occurs most frequently.)
If no number in a set occurs more than once, there is no mode for that set of data. It’s also possible for a data set to have two modes. This is known as bi-modal distribution.
Ex. 2.
- For the data set 1, 1, 2, 5, 6, 6, and 9 the mode is 1 and also 6.
- For the data set 2, 10, 24, 23, 23, 38, 38
- Both 23 and 38 appear twice each, making them both a mode for the data set above.
- (Bi-modal distribution occurs when there are two numbers that are tied in frequency.)
Similar to mean and median, the mode is used as a way to express information about random variables and populations.
As is evident from this example, it is important to take all manners of statistical values into account when attempting to draw conclusions about any data sample.
Use of Mean, Median and Mode
Each measure of central tendency has its own strengths and weaknesses. Here are a few to consider.
- The mean utilizes all numbers in a set to express the measure of central tendency. However, outliers – or data that lies well outside of the data set – can distort the overall measure. For example, a couple of extremely high scores can skew the mean, so the average score appears much higher than most of the scores actually are.
- The median gets rid of outliers or disproportionately high or low scores. At the same time, this could be an issue because it may not adequately represent the full set of numbers.
- The mode may be less influenced by outliers as well and is good at representing what is ‘typical’ for a given group of numbers. But it also may be less useful in cases where no number occurs more than once.
- While they are all measures of central tendency, each one looks at this tendency from a slightly different point of view. Whether to use the mean, median, or mode, depends on the data scores themselves.
- If there are no outliers in the data set, the mean may be the best choice in terms of accuracy since it takes into account each individual score and finds the average. Conversely, if outliers exist, the median or mode may be more accurate since the results won’t be skewed.
- Also, there is a need to consider what is to measure. If one is looking for the average (the mean) if one wants to identify the middle score (the median) or looking for the score that appears most often (the mode).